class: center, middle # Nearest Neighbor CS534 - Machine Learning Yubin Park, PhD --- class: center, middle Consider $$ y_1 = f(\mathbf{x}_1) $$ and $$ y_2 = f(\mathbf{x}_2) $$ --- class: center, middle If $$ \mathbf{x}_1 = \mathbf{x}_2 $$ then $$ y_1 = y_2 $$ --- class: center, middle What if $$ \mathbf{x}_1 \approx \mathbf{x}_2 $$ then $$ y_1 \approx y_2 \text{?}$$ --- ## Distance Metric We need to "measure" how similar `\(\mathbf{x}_1\)` and `\(\mathbf{x}_2\)` are using a distance function. A distance function satisfies: 1. `\(d(\mathbf{x}_1, \mathbf{x}_2) \ge 0\)`, and `\(d(\mathbf{x}_1, \mathbf{x}_2) = 0\)` if and only if `\(\mathbf{x}_1=\mathbf{x}_2\)` 1. `\(d(\mathbf{x}_1, \mathbf{x}_2) = d(\mathbf{x}_2, \mathbf{x}_1)\)` (symmetric) 1. `\(d(\mathbf{x}_1, \mathbf{x}_2) \le d(\mathbf{x}_1, \mathbf{x}_3) + d(\mathbf{x}_3, \mathbf{x}_2)\)` (triangle inequality) Questions: - Is `\( (\mathbf{x}_1 - \mathbf{x}_2 )^T(\mathbf{x}_1 - \mathbf{x}_2 ) \)` a distance function? - How about `\(\frac{\mathbf{x}_1^T \mathbf{x}_2}{\|\mathbf{x}_1\| \|\mathbf{x}_2\|}\)` ([cosine similarity](https://en.wikipedia.org/wiki/Cosine_similarity))? - How about `\(1 - \frac{\mathbf{x}_1^T \mathbf{x}_2}{\|\mathbf{x}_1\| \| \mathbf{x}_2\|}\)` (1 - cosine similarity)? --- ## k-Nearest Neighbors (kNN) No training is needed for kNN. For a new data point `\(\mathbf{x}_{\text{new}}\)`, 1. For `\(i=0\)` to `\(n\)`, 1. Measure the distance between `\(\mathbf{x}_{\text{new}}\)` and `\(\mathbf{x}_{i}\)` 1. Select Top-k nearest neighbors 1. `\(\hat{y} = \frac{\sum \mathbf{x}_{nn}}{k}\)` kNN is an [instance-based learning](https://en.wikipedia.org/wiki/Instance-based_learning) (or memory-based learning). Question: - What is the effect of `\(k\)` on the bias and variance of the model? --- class: center, middle .figure-w500[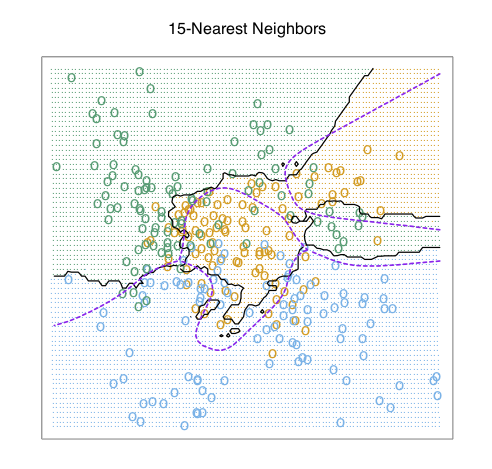] .reference[Chapter 13 of [ESLII](https://web.stanford.edu/~hastie/ElemStatLearn/)] --- class: center, middle .figure-w500[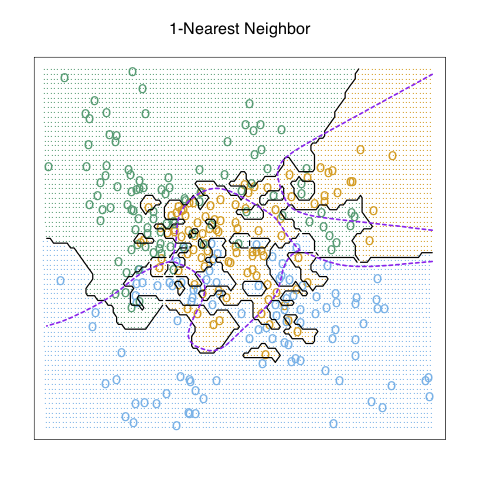] .reference[Chapter 13 of [ESLII](https://web.stanford.edu/~hastie/ElemStatLearn/)] --- class: center, middle .figure-w500[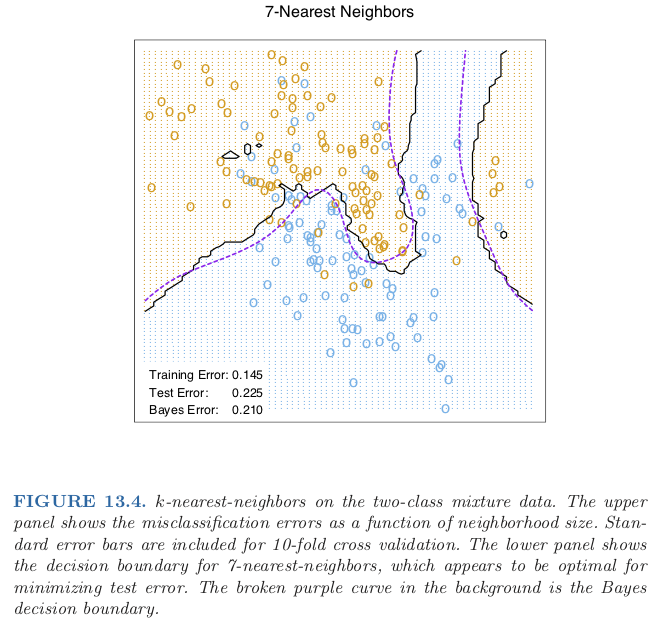] .reference[Chapter 13 of [ESLII](https://web.stanford.edu/~hastie/ElemStatLearn/)] --- class: center, middle .figure-w500[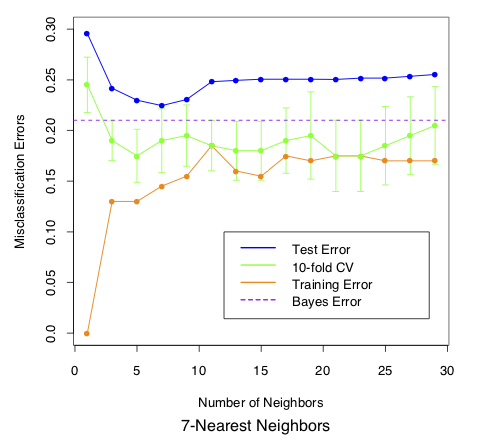] .reference[Chapter 13 of [ESLII](https://web.stanford.edu/~hastie/ElemStatLearn/)] --- ## Practical Considerations - Slow Preciction Speed - You need to scan all data points in the training set, `\(O(n)\)` - => [Approximate Nearest Neighbors](https://en.wikipedia.org/wiki/Nearest_neighbor_search#Approximate_nearest_neighbor) - Ambiguity of Metric - Which distance function should I choose? - => [Metric Learning](https://en.wikipedia.org/wiki/Similarity_learning) - Curse of dimensionality - Distances between sample pairs are about the same in high dimensional spaces - => [Dimensionality Reduction](https://en.wikipedia.org/wiki/Dimensionality_reduction) --- ## Approximate Nearest Neighbor We can make kNN a lot faster if we allow some mistakes. i.e. we will find `\(k\)` **near** neighbors, not the exact Top-k nearest neighbors. Hence, this algorithm is called Approximate Nereast Neighbors (ANN). The main technique is [Locality-sensitive Hashing](https://en.wikipedia.org/wiki/Locality-sensitive_hashing) (LSH). Simply speaking, 1. We want to have a function (LSH) that puts similar items to the same bucket with a high probability 1. For a new data point, we apply the function and finds the bucket that have similar data points to the data point 1. Find Top-k within the bucket Of course, there will be some False Positives and False Negatives... --- ## LSH Basic (1) Let's start with the cosine disimilarity: $$ d(\mathbf{x}_1, \mathbf{x}_2) = 1 - \frac{\mathbf{x}_1^T \mathbf{x}_2}{\lVert\mathbf{x}_1\rVert \lVert \mathbf{x}_2\rVert} $$ With a random vector `\(\mathbf{u}\)`, we will make a hash function as follows: $$ h_{\mathbf{u}}(\mathbf{x}) = \text{sign}(\mathbf{x}^T\mathbf{u})$$ In other words, the hash function returns either 1 or -1 (or 0) depending on the angle between `\(\mathbf{x}\)` and `\(\mathbf{u}\)`. Then, we have: $$ \text{Pr}(h\_{\mathbf{u}}(\mathbf{x}\_1)=h\_{\mathbf{u}}(\mathbf{x}\_2)) = 1 - \frac{\theta(\mathbf{x}_1, \mathbf{x}_2)}{\pi} \approx \cos(\theta(\mathbf{x}_1, \mathbf{x}_2)) $$ The probability of having the same hash value approximates their cosine similariity. This [random projection](https://en.wikipedia.org/wiki/Random_projection) hash is called [SimHash](https://en.wikipedia.org/wiki/SimHash). --- ## LSH Basic (2) Under SimHash, two items will be put in the same bucket if they are similar. More precisely, the more simialar those two are, the more likely they will be put in the same bucket. We have made 2 buckets using 1 SimHash. Are 2 buckets enough? To make `\(2^R\)` buckets, we use `\(R\)` random vectors: `\(\mathbf{u}_1, \mathbf{u}_2, \ldots, \mathbf{u}_R\)`. $$ h\_{\mathbf{U}} = (h\_{\mathbf{u}\_1}, h\_{\mathbf{u}\_2}, \ldots, h\_{\mathbf{u}\_R}) $$ ```python def simhash(x, U): """Returns an R length binary hash value.""" # x: a vector (m x 1) # U: a matrix (m x R) return "".join([str(int(h>0)) for h in np.dot(x, U)]) ``` --- ## LSH Basic (3) Then, the probability of two data points ending up in the same bucket is: $$ \text{Pr}(h\_{\mathbf{U}}(\mathbf{x}\_1)=h\_{\mathbf{U}}(\mathbf{x}\_2)) = s(\mathbf{x}_1, \mathbf{x}_2)^R $$ where `\(s(\mathbf{x}_1, \mathbf{x}_2)\)` represents the similarity between two points. And the probability that two data points will be put in different buckets: $$ \text{Pr}(h\_{\mathbf{U}}(\mathbf{x}\_1) \neq h\_{\mathbf{U}}(\mathbf{x}\_2)) = 1 - s(\mathbf{x}_1, \mathbf{x}_2)^R$$ Now, we have enough buckets to separate disimilar points. However, we have a new challenge. For a new data point, what if its corresponding bucket is empty? Or, even if it is not empty, but full of irrelevant data points? --- ## LSH Basic (4) Let's make multiple hash functions, `\(h_{\mathbf{U}_1}, h_{\mathbf{U}_2}, \ldots, h_{\mathbf{U}_B}\)`, and hope that at least one matched bucket is not empty. Since $$ \text{Pr}(h\_{\mathbf{U}}(\mathbf{x}\_1) \neq h\_{\mathbf{U}}(\mathbf{x}\_2)) = 1 - s(\mathbf{x}_1, \mathbf{x}_2)^R $$ we have: $$ \text{Pr}(h\_{\mathbf{U}\_b}(\mathbf{x}\_1) \neq h\_{\mathbf{U}\_b}(\mathbf{x}\_2), \forall b \in 1, \dots, B) = (1 - s(\mathbf{x}_1, \mathbf{x}_2)^R)^B $$ In other words, the probability of finding at least one bucket that has a neighbor candidate `\( \mathbf{x}_{\text{neighbor}}\)` with `\(s(\mathbf{x}_{\text{new}}, \mathbf{x}_{\text{neighbor}})\)`: $$ \text{Pr}(\text{hit}) = 1 - (1 - s(\mathbf{x}\_{\text{new}}, \mathbf{x}\_{\text{neighbor}})^R)^B $$ --- ## LSH Basic (5) Why are we doing this? So that we can find neighbors that are `\(s(\mathbf{x}_{\text{new}}, \mathbf{x}_{\text{neighbor}}) > t\)` with a very high probability. .center[.figure-350[]] --- ## LSH Toy Example (1) ```python R = 20 B = 5 def simhash(x, U): return "".join([str(int(h>0)) for h in np.dot(x, U)]) ``` ```python def fit(X, y, U_lst): n, m = X.shape B = len(U_lst) htab = [defaultdict(list) for b in range(B)] for i in range(n): x_i = X[i,:] y_i = y[i] for b in range(B): key = simhash(x_i, U_lst[b]) htab[b][key].append((x_i, y_i)) return htab ``` --- ## LSH Toy Example (2) ```python def predict(X, U_lst, htab): y_hat = [] n, m = X.shape B = len(U_lst) for i in range(n): x_i = X[i,:] y_hat_i = 0.0 for b in range(B): key = simhash(x_i, U_lst[b]) if key not in htab[b]: continue pairs = htab[b][key] X_nn = np.array([p[0] for p in pairs]) idx = np.argsort(np.dot(X_nn, x_i))[-1] y_hat_i = [p[1] for p in pairs][idx] break y_hat.append(y_hat_i) return y_hat ``` --- ## LSH Toy Example (3) ```python data = load_iris() scaler = StandardScaler() X = data.data y = (data.target == 1).astype(int) X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2) scaler.fit(X_train) X_train = scaler.transform(X_train) X_test = scaler.transform(X_test) n, m = X.shape U_lst = [np.random.randn(m, R) for b in range(B)] htab = fit(X_train, y_train, U_lst) y_hat = predict(X_test, U_lst, htab) acc = np.mean(y_hat == y_test) print(acc) ``` ```bash $ python lsh.py 0.9 ``` --- class: center, middle ## Questions?